Combinatorics Seminar-Doubly weighted rooted trees and computer networks
Thursday, September 26, 2019
6:15 pm - 11:59 pm
Title: Doubly weighted rooted trees and computer networks
Speaker: Geir Agnarsson, George Mason
Date and time: Thursday, September 26, 2:15–3:15pm
Place: Phillips 110
Date and time: Thursday, September 26, 2:15–3:15pm
Place: Phillips 110
Abstract: Let 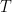 be a rooted tree with
be a rooted tree with 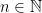 non-root vertices provided with two functions:
non-root vertices provided with two functions: 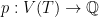 on the vertices and
on the vertices and  on the edges, and two fixed numbers
on the edges, and two fixed numbers 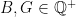 . We consider the Game-Over Attack Strategy (GOAS) of finding a rooted subtree
. We consider the Game-Over Attack Strategy (GOAS) of finding a rooted subtree 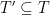 such that
such that 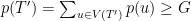 and
and  . In general, this decision problem is NP-complete, but that not the whole story. There are numerous special cases that can be solved in polynomial time in n, and these cases can be viewed as models for many security protocols in computer networks. The somber conclusion one can draw from this is that hacking into a computer system is theoretically easy! This is joint work with Ray Greenlaw and Sanpawat Kantrabutra.
. In general, this decision problem is NP-complete, but that not the whole story. There are numerous special cases that can be solved in polynomial time in n, and these cases can be viewed as models for many security protocols in computer networks. The somber conclusion one can draw from this is that hacking into a computer system is theoretically easy! This is joint work with Ray Greenlaw and Sanpawat Kantrabutra.

